In queste prime 4 immagini qui sotto potete vedere il risultato che si ottiene usando un quadrato al posto del triangolo come base di partenza per l'algoritmo di koch, la curva che viene generata assomiglia molto a quella ottenuta usando i triangoli.
vedi le prime 4 immagini qui sotto.
Ad ogni trasformazione ogni lato del quadrato si allunga di un terzo, come nel lato del triangolo iniziale di Koch, poichè anche questo lato viene diviso in tre parti uguali e la lunghezza della parte centrale viene raddoppiata grazie ai due lati del rettangolo senza una base che si viene a formare sollevando o facendo rientrare alternativamente il lato centrale del lato del quadrato e dato che la somma dei due lati minori del rettangolo è pari alla lunghezza della sezione centrale del lato, avremo perciò come nel caso dell'isola di Koch ogni lato del quadrato che si allunga di un terzo ad ogni iterazione

Ma se usiamo l'algoritmo una seconda volta, facendo proseguire la curva nel senso inverso, otteniamo una specie di collana di quadrati, anche se in questo modo non avremo più una linea continua come quella che caraterizza la curva di Koch.
Vedi le immagini qui sotto.
Se poi ripetiamo lo stesso trucchetto, ma inserendo un triangolo senza la base al posto di un rettagolo, avremo delle immagini come queste sotto.
La collana questa volta è formata da rombi, perchè unendo due triangoli equilateri senza la base si ottiene un rombo.
Le immagini che vedete qui sopra e qui sotto sono leggermente diverse perchè sono state ottenute, variando di poco la formula originale,
Le immagini sotto sono le cosidette SCATOLE DI KOCH le ho ottente usando usando il sistema IFS che è l'acronimo di Iterated Function System = Sistema di Funzioni Iterate. Il metodo è quello che abbiamo già visto con il triangolo di Sierpinki che si basava sulla simulazione di un'estrazione di un numero casuale.
img. 16
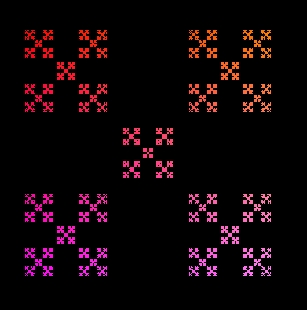
img. 17

img. 18

UN ALTRO MODO PER CALCOLARE LE DIMENSIONI FRATTALI
.... dei frattali.
Un altro modo per determinare il numero delle dimensioni è quello di usare una carta millimetrata trasparente oppure lo schermo del computer, per iniziare usiamo la carta.
Disegnamo una linea di 10 cm. su di foglio e lo copriamo con un altro foglio di carta millimetrata trasparente da 1 cm. è ovvio che la linea occupa 10 quadretti mentre se usiamo una carta millimetrata di 0,5 cm. i quadretti essendo grandi la metà, la stessa linea ne occuperà 20, perciò il numero dei quadretti raddoppia, ma la dimensione rimane = 1 perché è rappresentata dalla potenza alla quale bisogna elevare il numero dei quadretti = 20^1, se facciamo la stessa cosa con un quadrato o un rettangolo i quadretti necessari aumenteranno di un fattore 2^2 perchè se un quadrato occupa 10x10 = 100 quadretti della carta millimetrata da un cm, ne occupera 20^2 = 400 su una carta da 0,5 cm.

Dunque con la linea al dimezzare del lato dei quadretti della carta millimetrata, il numero dei quadretti raddoppia ma la dimensione rimane 1 perchè avremo 2^ 1 = una dimensione ; mentre con il quadrato il loro numero cresce a 2^ 2 = dimensioni; con lo stesso procedimento un cubo porta il numero delle dimensioni a 3 2^ 3 perchè per fare un cubo di 100 cm, di lato, occorrono 10^3 = 1000 cubetti da 10 cm.di lato mentre ne occorreranno 8000 con cubetti con un lato grande la metà, ossia 5 cm.di lato perchè il lato del cubo grande = 100 diviso per il lato del cubetto =5 da 20 e 20X20x20 20^ 3 = 8000.
Se applichiamo la stessa procedura alla figura frattale di Von koch quando dimezziamo il lato delle caselle della carta millimetrata, il loro numero aumenta di un fattore pari a 2^1,26 ossia ad una dimensione di 1,26 circa.

Questo metodo prende un po' più di tempo ma è più facile da afferrare.
Invece della carta potete usare il computer come ho fatto io con le due immagini qui a fianco,
Tanto per saperlo, la linea frattale della costa dell'Australia ha una dimensione di 1,13 mentre quella del Sudafrica è solamente di 1,04 la più frastagliata è quella della Norvegia con una dimensione di 1,52.
Con gli oggetti tridimensionali, usando un reticolo di cubi, troviamo che un cavolfiore ha una dimensione di 2,33 quello di un pezzo di carta appallottolato è di 2,5 con i polmoni umani raggiugiamo una dimensione di 2,97.
Da
L'equazione da un milione di dollari
Marcus du Sautoy ed. Rizzoli
Titolo originale
The number misteries. A mathematical odyssey through every day life
In questo caso si è usato un numero casuale compreso tra uno e cento, se il numero è inferiore a 25 accendi un pixel di un dato colore in una certo punto dello schermo, se il numero è inferiore a cinquanta, lo accendi con un secondo colore in un altro punto, se è inferiore a 75 in un'altro ancora e infine se è superiore a 75 lo accendi in un punto ancora diverso.
Il prossimo argomento sarà dedicato ai frattali ottenuti usando il sistema IFS, un lavoro di John Hutchinson e B. Mandelbrot, e sviluppata da Michael Barnsley.







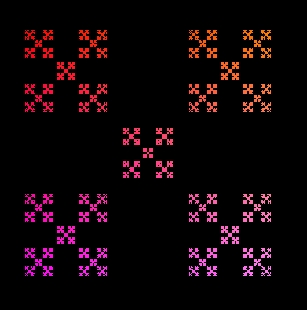


 Dunque con la linea al dimezzare del lato dei quadretti della carta millimetrata, il numero dei quadretti raddoppia ma la dimensione rimane 1 perchè avremo 2^ 1 = una dimensione ; mentre con il quadrato il loro numero cresce a 2^ 2 = dimensioni; con lo stesso procedimento un cubo porta il numero delle dimensioni a 3 2^ 3 perchè per fare un cubo di 100 cm, di lato, occorrono 10^3 = 1000 cubetti da 10 cm.di lato mentre ne occorreranno 8000 con cubetti con un lato grande la metà, ossia 5 cm.di lato perchè il lato del cubo grande = 100 diviso per il lato del cubetto =5 da 20 e 20X20x20 20^ 3 = 8000.
Se applichiamo la stessa procedura alla figura frattale di Von koch quando dimezziamo il lato delle caselle della carta millimetrata, il loro numero aumenta di un fattore pari a 2^1,26 ossia ad una dimensione di 1,26 circa.
Dunque con la linea al dimezzare del lato dei quadretti della carta millimetrata, il numero dei quadretti raddoppia ma la dimensione rimane 1 perchè avremo 2^ 1 = una dimensione ; mentre con il quadrato il loro numero cresce a 2^ 2 = dimensioni; con lo stesso procedimento un cubo porta il numero delle dimensioni a 3 2^ 3 perchè per fare un cubo di 100 cm, di lato, occorrono 10^3 = 1000 cubetti da 10 cm.di lato mentre ne occorreranno 8000 con cubetti con un lato grande la metà, ossia 5 cm.di lato perchè il lato del cubo grande = 100 diviso per il lato del cubetto =5 da 20 e 20X20x20 20^ 3 = 8000.
Se applichiamo la stessa procedura alla figura frattale di Von koch quando dimezziamo il lato delle caselle della carta millimetrata, il loro numero aumenta di un fattore pari a 2^1,26 ossia ad una dimensione di 1,26 circa.
 Questo metodo prende un po' più di tempo ma è più facile da afferrare.
Invece della carta potete usare il computer come ho fatto io con le due immagini qui a fianco,
Tanto per saperlo, la linea frattale della costa dell'Australia ha una dimensione di 1,13 mentre quella del Sudafrica è solamente di 1,04 la più frastagliata è quella della Norvegia con una dimensione di 1,52.
Con gli oggetti tridimensionali, usando un reticolo di cubi, troviamo che un cavolfiore ha una dimensione di 2,33 quello di un pezzo di carta appallottolato è di 2,5 con i polmoni umani raggiugiamo una dimensione di 2,97.
Da
L'equazione da un milione di dollari
Marcus du Sautoy ed. Rizzoli
Titolo originale
The number misteries. A mathematical odyssey through every day life
Questo metodo prende un po' più di tempo ma è più facile da afferrare.
Invece della carta potete usare il computer come ho fatto io con le due immagini qui a fianco,
Tanto per saperlo, la linea frattale della costa dell'Australia ha una dimensione di 1,13 mentre quella del Sudafrica è solamente di 1,04 la più frastagliata è quella della Norvegia con una dimensione di 1,52.
Con gli oggetti tridimensionali, usando un reticolo di cubi, troviamo che un cavolfiore ha una dimensione di 2,33 quello di un pezzo di carta appallottolato è di 2,5 con i polmoni umani raggiugiamo una dimensione di 2,97.
Da
L'equazione da un milione di dollari
Marcus du Sautoy ed. Rizzoli
Titolo originale
The number misteries. A mathematical odyssey through every day life